МАЙЕР Р.В.

ПРОВЕРКА ПРИНЦИПА ЭКСТРЕМАЛЬНОГО ДЕЙСТВИЯ ГАМИЛЬТОНА МЕТОДОМ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

1. Принцип экстремального действия Гамильтона. Одним из фундаментальных принципов классической механики является принцип экстремального действия [1, 2, 3]: движение системы из положения в пространстве конфигураций в положение происходит таким образом, что действие



при фиксированных начальном и конечном моментах времени достигает экстремального значения. Подынтегральная функция равна разности кинетической и потенциальной энергий системы


где -- число степеней свободы. Она называется функцией Лагранжа или лагранжианом.

Действие экстремально, когда его вариация равна нулю: Принцип Гамильтона можно сформулировать иначе: механическая система в промежутке времени от до движется так, что вариация действия равна нулю.

Проверка принципа экстремального действия состоит в сравнении значений действия для действительного и окольных путей перемещения системы из начального положения в конечное. Она принципиально не может быть выполнена экспериментально по двум причинам: 1) система просто не будет двигаться по окольному пути: из бесконечного множества путей она выберет именно тот, для которого действие экстремально; 2) отсутствует прибор для измерения действия , соответствующего тому или иному пути перехода системы из одного состояния в другое. Поэтому для проверки приниципа Гамильтона следует провести численный эксперимент, в ходе которого осуществляется вычисление и сравнение действия для действительного и окольных путей.

2. Основная идея вычислительного эксперимента. Рассмотрим простую механическую систему, например, частицу в силовом поле. Исходя из основного закона динамики и законов сохранения, определим характер движения системы, а также время перехода из положения в положение . Создадим цикл, в котором с некоторым шагом варьируется зависимость , определяющая движение частицы из положения в положение при фиксированном времени . При этом частица может двигаться как по другой, так и по той же траектории, -- путь в пространстве будет каждый раз различным.

В этом цикле должно быть предусмотрено нахождение величины , соответствующее данному пути движения системы, осуществляемое путем численного интегрирования, и вывод результата вычислений на экран в цифровом или графическом виде. Предполагается, что действие , соответствующее движению системы по действительному пути всегда меньше, чем по окольным путям. Ниже рассмотрено решение этой задачи для одномерного и двумерного движения частицы.

3. Моделирование одномерного движения частицы. Рассмотрим частицу массой кг, движущуюся в однородном гравитационном поле с напряженностью  Н/кг. Ось направим вверх. Пусть в начальный момент времени частица имеет направленную вверх скорость 10 м/с и координату .

Из основного закона динамики следует . Дважды интегрируя, получаем:

Постоянные интегрирования определяются из начальных условий: м/с, Отсюда следует, что м/с, м/с, . Итак, скорость и координата точки


Конечным будем считать момент с, когда точка имеет нулевую скорость, а ее координата  м. Движению по действительному пути соответствует график , нарисованный жирной линией (рис.1).

Рис. 1. Рис. 2.

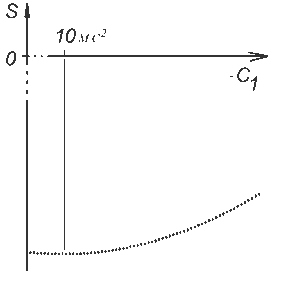
Вычислим действие при движении точки по действительному пути, учитывая, что лагранжиан системы равен


Имеем:


(Джс).

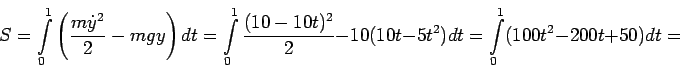
Необходимо варьировать функцию так, чтобы в моменты времени и c система находилась в положениях и  м соответственно. То есть должны выполняться ограничения

Так как , то первое уравнение приводит к тождеству. Подставляя во второе уравнение с, получаем уравнение, связывающее коэффициенты $C_1$ и

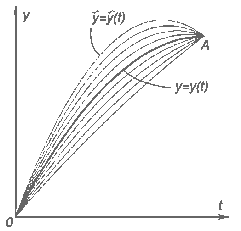
Если с некоторым шагом изменять $C_2$, то можно, вычисляя , построить графики , соответствующий окольным путям движения системы при фиксированном времени . Эти графики изображены на рис.1 тонкими линиями.

Разработанная нами программа позволяет, исходя из значения определить и вычислить действие Результаты подобных расчетов представлены в таблице 1.

Таблица 1
, м/с -9,0 -9,5 -9,8 -10,0 -10,2 -10,5 -11,0
, м/с 9,50 9,75 9,90 10,00 10,10 10,25 10,50
, Джс -16,625 -16,656 -16,665 -16,667 -16,665 -16,656 -16,625

Из таблицы видно, что минимального значения Джс действие достигает при м/с и =10 м/с, что соответствует движению по действительному пути. При движении системы по окольным путям значение больше. Малые вариации действительного пути приводят к изменениям действия на величину более высокого порядка малости. В самом деле, при относительном изменении на 2% (от до м/с) относительное изменение действия составляет 0,067% (от до Дж с), что на порядок меньше.

График зависимости действия от вариации одного из коэффициентов уравнения движения системы показан на рис.2. Видно, что действительному движению системы соответствует минимальное действие. При малых вариациях действительного пути действие изменяется на величину более высокого порядка малости.

4. Моделирование двумерного движения частицы. Рассмотрим движение частицы из области с потенциалом в другую область с потенциалом . Допустим, имеются две горизонтальные прямоугольные пластины, расположенные на разных высотах, сопряженные плавным переходом -- горкой. С одной пластины на другую перекатывается шарик массой . Пусть нулевой уровень потенциальной энергии совпадает с уровнем нижней пластины , тогда потенциальная энергия шарика на верхней пластине равна При переходе шариком границы раздела областей происходит резкое изменение направления движения (рис.3). Подобное "преломление" траектории наблюдается при переходе электрона через границу раздела двух областей с различными потенциалами электрического поля.

Рис. 3. Рис. 4.

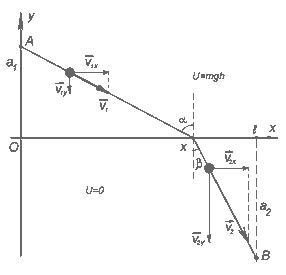
Выберем систему координат, как показано на рис.3. Скорости до и после "преломления" связаны соотношением: 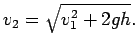Так как то шарик движется по траектории, для которой Соответствующая координата точки "преломления" траектории равна

Время движения составляет


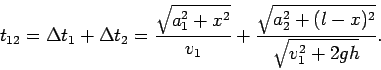
Первая часть разработанной программы, исходя из заданных вычисляет время движения шарика по действительному пути. Вторая часть программы содержит цикл, в котором с некоторым шагом изменяется координата точки "преломления" траектории, вычисляется время 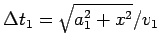и движения шарика по верхней и нижней пластинам, определяется скорость 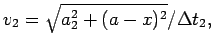и определяется действие по формуле


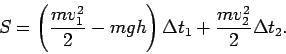
В цикле также предусмотрено построение графиков либо вывод результатов вычислений этих функций в цифровом виде.

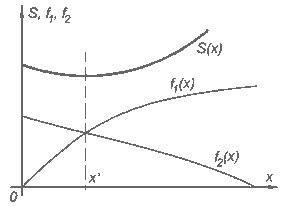
Результат работы программы представлен на рис.4. Видно, что действие достигает минимума при таком , при котором графики функций пересекаются. Это означает, что выполняется соотношение соответствующее действительному движению системы.

Разработанная методика проверки принципа экстремального действия Гамильтона может быть использована в рамках курсов "Компьютерное моделирование" и "Теоретическая физика: Классическая механика".

ЛИТЕРАТУРА

  1. Беленький И.М. Введение в аналитическую механику.-- М.: Высшая школа, 1964.-- 323 с.
  2. Жирнов Н.И. Классическая механика.-- М.: Просвещение, 1980.-- 303 с.
  3. Ландау Л.Д., Лифшиц Е.М. Механика.-- М.: Наука, 1965.-- 203 с.


Майер Р.В. Проверка принципа экстремального действия Гамильтона методом численного моделирования // Проблемы учебного физического эксперимента: Сборник научных трудов. Выпуск 20.--- М.: ИОСО РАО, 2004.--- C. 82--86.