ЭКСПЕРИМЕНТАЛЬНОЕ ДОКАЗАТЕЛЬСТВО ВТОРОГО НАЧАЛА ТЕРМОДИНАМИКИ
Одним из сложнейших вопросов современного курса физики является необратимость физических явлений. Трудность усвоения этого материала школьниками понятна: они не знакомы с понятием вероятности и законами сложения и умножения вероятностей. Поэтому желательно, чтобы изучение этой темы опиралось на простой эксперимент, позволяющий одновременно ввести понятие вероятности события и убедиться в том, что состояния системы с максимальным беспорядком являются наиболее вероятными. Это позволило бы подтвердить второе начало термодинамики [1, c.261]: "В замкнутой и адиабатически изолированной макроскопической системе наиболее вероятным является процесс, сопровождающийся возрастанием энтропии".
1. Традиционная методика. В учебнике [2] за 10 класс для школ и классов с углубленным изучением физики при изучении необратимости физических явлений предлагается рассмотреть сосуд, разделенный перегородкой на две половины, одна из которых заполнена газом. Если открыть перегородку, то газ равномерно распределится по всему объему сосуда, то есть система перейдет из упорядоченного состояния в неупорядоченное состояние, характеризуемое большей энтропией. Для доказательства того факта, что неупорядоченные состояния имеют большую вероятность, авторы рассматривают следующий мысленный эксперимент.
Пусть газ состоит из 6 молекул. Тогда система имеет 64 различных состояния, при которых те или иные молекулы находятся в правой и левой половинках сосуда. Изготовим 64 карточки, соответствующие этим состояниям, поместим их в коробку и будем вытаскивать по одной, каждый раз возвращая карточки обратно. В этом случае чаще будут попадаться карточки, соответствующие равномерному распределению молекул в сосуде, потому что их больше.
Приведенные выше рассуждения будут убедительны только для тех учащихся, которые уже выполняли аналогичные процедуры с многократно повторяющимся случайным процессом и задумывались об этом. И даже для них может показаться непонятным, почему для системы из 6 молекул используются 64 карточки, а не семь, соответствующих состояниям, когда в одной из половинок сосуда одновременно находятся 0, 1, 2, 3, 4, 5 или 6 молекул. Для других учащихся результат этого мысленного эксперимента может показаться неочевидным, а его связь с рассматриваемой проблемой абсолютно непонятной.
Таким образом, необходима постановка простого эксперимента, позволяющего убедиться в том, что наиболее вероятными являются состояния системы с максимальной неупорядоченностью. Его методика изложена ниже.
2. Моделирование молекул монетами. Вместе с рассмотрением различных физических процессов, таких как диффузия, расширение газа в вакуум, предлагается выполнить с учащимися следующий эксперимент, непосредственно доказывающий, что вероятность наименее упорядоченного состояния системы максимальна.
Учитель, рассматривая газ из 6 молекул, утверждает, что попадание той или иной молекулы в левую или правую половины сосуда -- такой же случайный процесс, как и падение монетки на "орла" или "решку". Значит поведение системы из 6 хаотически движущихся молекул можно смоделировать 6 одинаковыми монетками, случайным образом переворачивающимися в банке, если ее потрясти. При этом, учащиеся видят, как в баночку учитель кладет шесть монет и несколько раз встряхивает ее. Процесс нахождения положения молекул в сосуде в этом случае аналогичен определению количества монет, упавших на ту или иную сторону. Для определенности будем считать, что монета, упавшая на "орла", означает попадание соответствующей молекулы в левую половину сосуда.
3. Как проводить опыт. Для регистрации результатов опыта учитель на доске и учащиеся в тетрадях заготавливают таблицы, аналогичные табл.1. В первом столбце указывается состояние системы, во втором отмечаются количества случаев, когда система находилась в том или ином состоянии, в третьем -- вероятность этого события.
С целью уменьшения длительности эксперимента, бросание монеток можно доверить нескольким учащимся. Учащиеся встряхивают монеты в руках, затем бросают их на поверхность стола и сообщают классу о количестве монет, упавших "орлом" вверх. Учитель, а вместе с ним и весь класс ставят в соответствующей строке "+", после чего все повторяется снова. Для получения убедительных результатов достаточно произвести 30-100 опытов.
Таблица 1
| Состояние | Число состояний | Вероятность |
| 0 -- 6 | ++ | 2% |
| 1 -- 5 | +++++++++ | 9% |
| 2 -- 4 | ++++++++++++++++++++++++++ | 26% |
| 3 -- 3 | +++++++++++++++++++++++++++++ | 29% |
| 4 -- 2 | +++++++++++++++++++++ | 21% |
| 5 -- 1 | ++++++++++ | 10% |
| 6 -- 0 | +++ | 3% |
Затем подсчитывается вероятность нахождения системы в том или ином состоянии как отношение числа плюсов в данной строке к их общему числу и записывается в третий столбец.
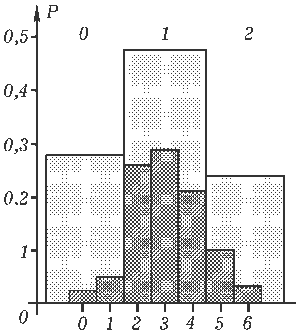
На рис.1 темным цветом представлена гистограмма распределения эмпирических вероятностей по различным состояниям системы, полученная в описанном выше опыте с шестью монетами. Из него видно, что максимальная вероятность соответствует наиболее неупорядоченному состоянию системы, при котором три молекулы находятся в левой половине сосуда, а три других молекулы -- в правой. Наиболее упорядоченным состояниям системы, при которых все молекулы газа находятся в одной половине сосуда, соответствуют вероятности, близкие к нулю.

4. А если молекул много? Если повторить опыт с четырьмя или двумя монетами, то можно обнаружить, что соответствующие кривые будут иметь менее ярко выраженный максимум. Это видно из рис.1, на котором приведена также гистограмма распределения вероятностей системы по различным ее состояниям в опыте с двумя монетами. Сравнивая эти две гистограммы, можно заметить, что чем больше монет используется в опыте, тем сильнее отличаются вероятности, соответствующие наиболее и наименее упорядоченным состояниям.
Отсюда следует, что чем больше молекул содержит система, тем сильнее отличаются вероятности ее нахождения в абсолютно беспорядочном и упорядоченном состояниях. В реальной ситуации количество молекул в сосуде настолько велико, что максимум, приходящийся на их равномерное (то есть беспорядочное) распределение, получается очень острым, а вероятность обнаружения упорядоченного состояния -- близкой к нулю.
Среди физиков по этому поводу ходит шутка. Представим себе дюжину обезьян, которые сидят перед печатными машинками и случайным образом бьют по клавишам. Вероятность того, что все молекулы в сосуде, двигаясь хаотически, вдруг соберутся в одной из его половин, столь же мала, как вероятность того, что из напечатанных обезьянами листов получится нескольких томов Британской энциклопедии.
5. Попробуйте сами. Подчеркнем, что понятие энтропии как меры беспорядка так же успешно применимо к системе из 6 монет, как и к газу. В принципе вопрос о необратимости явлений можно корректно изложить, не рассматривая расширение газа, а исследуя поведение системы, состоящей из большого количества хаотически движущихся макроскопических объектов. В этом смысле описанные выше опыты не являются модельными.
Нами рассмотрена модель процесса расширения газа в вакуум и проанализированы вероятности различных состояний системы. А что если газ не один, а их два? Как доказать, что вероятность состояния системы, наступающего после диффузии, при котором молекулы обоих газов равномерно распределены по всему объему, максимальна? Для этого уже потребуются монеты различного достоинства, диаметра или цвета. Попробуйте самостоятельно выполнить эти опыты.
Представленные эксперименты и рассуждения настолько наукоемки, что могут быть проведены в рамках фронтальной лабораторной работы или работы физического практикума. При ограниченности времени на уроке учитель может дать задание провести опыты с монетками дома. Нами данная методика апробирована в классе из 34 учащихся, причем каждая парта участвовала в проведении опыта. Объяснение условий эксперимента, регистрация его результатов и их анализ заняли около 15 минут. Положительным моментом явилось также то, что каждый из учащихся принимал участие в эксперименте, влияя на его результат, а не пассивно наблюдал за проведением опыта учителем.
ЛИТЕРАТУРА