Майер Р.В. Информатика: Кодирование информации. Принципы работы ЭВМ --- Учебн. пособ. для вузов. --- Глазов: ГИЭИ филиал ИжГТУ, 2004. -- 24 c.

ВВЕДЕНИЕ

Информатика -- наука, изучающая общие свойства информации, процессы ее хранения и обработки, методы создания информационных систем и технологий. Виды информационных процессов: создание новой информации, преобразование, уничтожение и передача информации.

Информатика изучает: 1) устройство ЭВМ, технические средства, используемые для обработки информации; 2) алгоритмические средства, алгоритмы решения различных задач; 3) программные средства, програмное обеспечение ЭВМ. Информатика -- это: 1) отрасль народного хозяйства (создание технических и программных средств); 2) фундаментальная наука (методология и теория создания информационных систем и технологий); 3) прикладная дисциплина (изучение информационных процессов, разработка информационных моделей, систем и технологий).

Задачи информатики: 1) исследование информационных процессов любой природы; 2) разработка информационной техники и создание новейшей технологии переработки информации; 3) использование компьютерной техники и технологии во всех сферах общественной жизни.

Информационное общество -- общество, в котором большинство людей заняты производством, хранением, переработкой и реализацией информации. Критерии развитости: наличие компьютеров, развитие рынка программного обеспечения, функционирование компьютерных сетей. Информационная культура -- умение работать с информацией, используя для ее получения, обработки и передачи компьютерную технологию, современные технические средства и методы.

Информационная революция -- качественные изменения в методах обработки информации, приводящие к преобразованию общественных отношений. В истории человеческого общества произошло несколько информационных революций: 1) изобретение письменности (передача знаний от поколения к поколениям); 2) изобретение книгопечатания, (изменило индустриальное общество, культуру, организацию деятельности); 3) изобретение телеграфа, телефона, радио, телевидения (позволило оперативно передавать информацию); 4) изобретение микропроцессорной технологии и ЭВМ (создание компьютеров, компьютерных сетей).

Развитие вычислительной техники начинается с первой счетной машины Паскаля (1642 г.), суммирующей десятичные числа. Машина Лейбница (1673 г.) выполняла все четыре арифметических действия. Она стала прототипом арифмометров (1820-1960 гг.) Идея создания программно-управляемой счетной машины, имеющей арифметическое устройство, устройство управления, устройства ввода информации и печати, была выдвинута Бэббиджем (1822 г.).

Изобретение электронных ламп, транзисторов, интегральных схем (ИС) предопределили появление и развитие ЭВМ. Поколения ЭВМ:

1 поколение (1951-1954): электронные лампы, ОЗУ на ЭЛТ, емкость ОЗУ 100 байт, быстродействие $10^3-10^4$ оп/с, пульт управления и перфокарты.

2 поколение (1958-1960): транзисторы, ОЗУ на ферритовых сердечниках, емкость ОЗУ 1000 байт, быстродействие $10^6$ оп/с, перфокарты и перфоленты.

3 поколение (1965-1976): интегральные схемы (ИС), ОЗУ на ферритовых сердечниках, емкость ОЗУ $10^4$ байт, быстродействие $10^7$ оп/с, для ввода и вывода информации используется алфавитно-цифровой терминал.

4 поколение (1976-1985): большие и сверхбольшие ИС, ОЗУ на БИС и СБИС, емкость ОЗУ -- $10^5-10^7$ байт, быстродействие -- $10^8-10^9$ оп/с, монохроматический и цветной графический дисплей, клавиатура, мышь и др.

5 поколение (1986- ... ): опто- и криоэлектроника, ОЗУ на СБИС, емкость ОЗУ $10^8$ байт, быстродействие $10^{12}$ оп/с, цветной дисплей, клавиатура, мышь, мультимедиа, устройство голосовой связи с ЭВМ и др.

1. ИНФОРМАЦИЯ И ЕЕ КОДИРОВАНИЕ

1.1. Информация и ее свойства. Датчик, измеряющий физическую величину, создает электрический сигнал. Данные -- это зарегистрированные сигналы. Методы регистрации: перемещение тел, изменение формы, поверхности, электрических, магнитных и оптических характеристик носителя информации, изменение состояния электронной системы и т.д. Основные операции с данными: сбор, формализация, фильтрация, сортировка, архивация, защита, передача, преобразование.

Пусть выход датчика в зависимости от измеряемой величины может принимать $n$ различных состояний. Каждый акт измерения является опытом с $n$ исходами, результат которого заранее неопределен. Аналогично, при формировании сообщения каждый символ выбирается из алфавита, содержащего $n$ букв, что может рассматриваться как опыт с $n$ исходами.

Проведение опыта (получение сообщения) снижает неопределенность наших знаний об объекте. Если опыт имеет $n$ исходов, то мерой неопределенности является функция $H(n)$, зависящая от числа исходов. Если $n=1$, то неопределенность отсутствует и $H(n)=0$, с ростом $n$ функция $H(n)$ возрастает. Рассмотрим два независимых опыта $\alpha$ и $\beta$ с числом равновероятных исходов $n_\alpha$ и $n_\beta .$ Сложный опыт, состоящий в одновременном выполнении опытов $\alpha$ и $\beta$ имеет $n_\alpha\cdot n_\beta$ равновероятных исходов (то же самое относится к сообщению из двух символов). Итак, мера неопределенности сложного опыта должна быть равна сумме мер неопределенностей опытов $\alpha$ и $\beta$: $H(n_\alpha\cdot n_\beta)=H(n_\alpha )+ H(n_\beta )$. Перечисленным требованиям удовлетворяет функция $H(n)=log_a(n),$ которая называется энтропией. Если $a=2,$ то единицей измерения является бит, (binary digit) если $a=10,$ то дит.

В опыте, имеющем $n$ равновероятных исходов, вероятность каждого из них $p=1/n.$ На долю каждого из $n$ исходов приходится энтропия $H_1=(1/n)\log_2 n=-(1/n)\log_2 (1/n)=-p log_2 p$. Найдем количество информации, получаемой при выборе одного из двух равновероятных исходов: $ H=1/2 \log_2 2+1/2 \log_2 2=1 $ (бит).

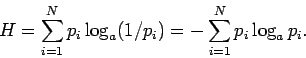
Энтропия опыта с $n$ неравновероятными исходами определяется формулой Шеннона (1948 г.): \begin{displaymath}H=\sum_{i=1}^N p_i \log_a(1/p_i)=-\sum_{i=1}^N p_i \log_a p_i. \end{displaymath}

где $p_i=1/n$ -- вероятность $i$-ого исхода. Например, для опыта с двумя исходами, вероятности которых $p_1=0,3$ и $p_2=0,7$ энтропия равна $H=-(0,3*\log_2 0,3+0,7*\log_2 0,7)= 0,88$ бит, то есть меньше 1 бит.

Пусть до получения информации имеются некоторые предварительные сведения об объекте $\alpha$. Мерой нашей неосведомленности является функция $H(\alpha )$, которая в то же время служит и мерой неопределенности состояния объекта. После получения некоторого сообщения $\beta$ получатель приобрел некоторую дополнительную информацию $I_{\beta }(\alpha )$, уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения $\beta$) неопределенность состояния объекта стала $H_{\beta }(\alpha )$.

Тогда количество информации $I_{\beta }(\alpha )$ об объекте, полученной в сообщении $\beta$, определяется так: $I_{\beta}(\alpha)=H(\alpha) - H_{\beta}(\alpha),$ то есть количество информации равно уменьшению неопределенности состояния системы (убыли энтропии).

Если после сообщения неопределенность обратилась в ноль $H_{\beta}(\alpha)=0$), то первоначальное неполное знание заменится полным знанием и количество информации в сообщении равно начальной энтропии $I_{\beta}(\alpha)=H(\alpha).$ Иными словами, энтропия объекта $H(\alpha )$ может рассматриваться как мера недостающей информации.

Свойства информации (энтропии): 1) информация (энтропия) сложного опыта (сообщения) равна сумме информаций (энтропий) его частей; 2) при том же числе исходов наибольшую информацию (энтропию) имеет опыт (сообщение) с равновероятными исходами. Требования к информации: достоверность, полнота, актуальность, полезность, понятность, адекватность.

1.2. Метод измерения информации. Рассмотрим алфавит из $m$ символов, где $p_i$ ($i=1, 2, 3 ..., m$) -- вероятность выбора из алфавита $i-$ой буквы для кодирования сообщения. Каждый такой выбор уменьшает степень неопределенности сообщения, увеличивая количество информации. Среднее количество информации, сообщаемое при выборе одного символа, согласно формуле Шеннона, равно:

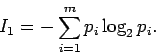
\begin{displaymath}I_1=- \sum\limits_{i=1}^{m} p_i \log_2 p_i.\end{displaymath}

Если выбор каждой буквы равновероятен, то $p_i=1/m.$ Подставляя это значение, получим, что каждый символ несет информацию:

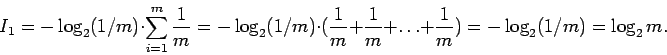
В ЭВМ информация кодируется числовыми кодами. Если система счисления имеет основание $m$, то числу разрядов $n$ соответствует разное количество $N$ комбинаций цифр ($N=m^n$). Если $m=2, n=4,$ то $N=2^4=16: 0000, 0001, 0010, 0011 ..., 1111,$ то есть в 4 разрядах может быть записано $I=\log_2 16=4$ бит.

При представлении информации в виде последовательности символов 0 и 1, раскодирование возможно при наличии соглашения о фиксированной длине последовательностей из 0 и 1, составляющих слово. Такой длиной принято считать восемь символов (0 и 1) -- 8 бит или байт. Более крупные единицы:
1 Кбайт=1024 байта=$2^{10}$ байт, 1 Мбайт=1024 Кбайта=$2^{20}$ байт,
1 Гбайт=1024 Мбайта=$2^{30}$ байт, 1 Тбайт=1024 Гбайта=$2^{40}$ байт
($2^{10}=1024_{10}=10000000000_2$).

В восьми разрядах (байте) можно записать 256 различных целых двоичных чисел, что достаточно чтобы дать неповторяющееся обозначение каждой заглавной и строчной букве русского и английского алфавитов, цифрам, знакам препинания, всем символам на клавиатуре компьютера. Таблица кодирования символов 8-битовыми числами называется кодовой таблицей символов ASCII (American Standart Code for Information Interchange), она представлена на обложке.

1.3. Системы счисления. Информация в ЭВМ кодируется в двоичной, двоично-десятичной или в шестнадцатиричной системе счисления. Система счисления -- это способ наименования и изображения чисел с помощью цифр, то есть символов, имеющих определенные количественные значения.

В позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе. Количество $P$ различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в пределах от 0 до $P-1.$ Числа в системе счисления с основанием $P$ равны:

\begin{displaymath}a_{r-1} P^{r-1}+a_{r-2} P^{r-2}+...+a_1 P^1+a_0P^0+ a_{-1} P^{-1}+a_{-2} P^{-2}+...+a_{-s} P^{-s}, \end{displaymath}

где нижние индексы определяют месторасположение цифры в числе, $r$ и $s$ -- количества разрядов для записи целой и дробной части числа соответственно.

Максимальное целое число, которое может быть представлено в $r$ разрядах: $N_{max}= P^r-1.$ Минимальное значащее (не равное 0) число, которое можно записать в $s$ разрядах дробной части: $N_{min}=P^{-s}.$ Имея в целой части числа $r$, а в дробной $s$ разрядов, можно записать всего $P^{r+s}$ разрядных чисел. Диапазон значащих чисел $N$ в системе счисления с основанием $P$ при наличии $r$ разрядов в целой части и $s$ разрядов в дробной части (без учета знака числа) будет: $P^{-s}\le N\le P^{r}-P^{-s}.$ При $P=2, r=10, s=6$ имеем: $2^{-6}\le N\le 1024-1.$

Чем больше основание $P$ тем больше затраты на изображение цифры, но меньше разрядов требуется для изображения одного и того же числа. Наиболее эффективной является использование троичной системы счисления.

Десятичная система счисления ($P=10$) используется при ручном счете. $ 157,43_{10}=1*10^2+5*10^1+7*10^0+4*10^{-1}+3*10^{-2}. $

Таблица двоичных кодов десятичных и шестнадцатеричных цифр.

DEC BIN HEX DEC BIN HEX DEC BIN HEX DEC BIN HEX
0 0000 0 4 0100 4 8 1000 8 12 1100 C
1 0001 1 5 0101 5 9 1001 9 13 1101 D
2 0010 2 6 0110 6 10 1010 A 14 1110 E
3 0011 3 7 0111 7 11 1011 B 15 1111 F

Шестнадцатиричная система счисления -- основание $P=16.$ Используются цифры от 0 до 9 и буквы $A$=10, $B$=11, $C$=12, $D$=13, $E$=14, $F$=15. Восемь двоичных разрядов (байт) могут быть представлены только двумя шестнадцатиричными разрядами (1 байт = 8 битов, то есть $2^8=(16)^2=256$ комбинаций).

Двоично-десятичное представление -- представление десятичного числа при котором каждая цифра отдельно кодируются четырьмя двоичными цифрами и в таком виде записываются последовательно друг за другом. Двоично-десятичная запись более длинная, но в ней удобнее производить арифметические действия и выводить числа на экран.

Пример: 1) Перевод двоичного числа в десятичное: $101110,101_{(2)}=1*2^5+0*2^4+1*2^3+ 1*2^2+1*2^1+0*2^0+1*2^{-1}+0*2^{-2}+ 1*2^{-3}=46,625_{(10)}.$ 2) Перевод шестнадцатиричного числа в двоичное: $F17B_{16} = 1111000101111011_2.$ 3) Перевод десятичного числа в двоично-десятичное: $ 9703_{10}= 1001 0111 0000 0011_{2-10}.$

1.4. Кодирование целых положительных чисел. Кодирование -- преобразование состояния $X_i$ системы в сообщение $Y_j$ посредством некоторого оператора $P$: $Y_j=P(X_i)$, где $X=(X_1, X_2, \ldots X_n),$ $Y=(Y_1, Y_2, \ldots Y_m)$ -- конечные множества состояний системы и соответствующих им сообщений (знаков в алфавите).

Система кодирования -- правила кодового обозначения объектов, используемые для удобной и эффективной обработки информации. Вся информация (данные и команды) представлена в виде двоичных кодов. Ячейка памяти ОЗУ, к которой можно обратиться, имеет длину 1 байт. Каждый байт ОЗУ имеет свой адрес. Поле -- последовательность битов в определенном формате, имеющая некоторый смысл. Машинное слово -- наибольшая последовательность разрядов (бит), которую ЭВМ может обрабатывать как единое целое. Его длина зависит от разрядности процессора (16, 32, 64 бита). Различают слово, полуслово, двойное слово.

Если длина машинного слова 16 бит, то наибольшее целое число, которое может быть в них записано равно $2^{16}-1=111111111111111=65535_{10}$, а наименьшее -- 0. В языке Pascal такие числа определены как Word. Числа типа Longint занимают в памяти ЭВМ 4 байта.

Сложение и умножение производятся по правилам:

\begin{displaymath}0+0=0, \, 0+1=1, \, 1+0=1, \, 1+1=10, \, 0*0=0, \, 0*1=0, \, 1*0=0, \, 1*1=1.\end{displaymath}

1.5. Кодирование целых чисел со знаком. Прямой код двоичного числа включает в себя код знака (знак $+$ соответствует 0, знак $-$ - 1) и абсолютное значение этого числа:

\begin{displaymath}X_{10}=-13, \, \, X_2=-1101, \, \, [X_2]pr=1\vert 1101,\end{displaymath}


\begin{displaymath}X_{10}=9, \, \, X_2=1001, \, \, [X_2]pr=0\vert 1001.\end{displaymath}

Вертикальная линия отделяет знаковый разряд от абсолютного значения числа.

Обратный код положительных чисел такой же как и прямой код, в знаковом разряде -- 0. Для получения обратного кода отрицательного числа его разряды инвертируются (0 заменяется на 1 и наоборот), в знаковом разряде -- цифра 1:

\begin{displaymath}X_{10}=12, \, \, X_2=1100, \, \, [X_2]pr=[X_2]obr=0\vert 1100,\end{displaymath}

\begin{displaymath}X_{10}=-7, \, \, X_2=-0111, \, \, [X_2]obr=1\vert 1000.\end{displaymath}

Дополнительный код положительных чисел такой же как и прямой код. У отрицательных чисел дополнительный код равен результату суммирования обратного кода числа с единицей младшего разряда:

\begin{displaymath}X_{10}=18, \, \, X_2=10010, \, \, [X_2]pr=[X_2]obr=[X_2]dop=0\vert 10011, \end{displaymath}


\begin{displaymath}X_{10}=-11, \, \, X_2=-1011, \, \, [X_2]dop=[X_2]obr+1=1\vert100+1=1\vert101. \end{displaymath}

В ЭВМ разность $x_1-x_2$ находится так: оба числа переводятся в дополнительный код, затем складываются и единица в самом старшем разряде отбрасывается. То есть вычитание сводится к сложению, осуществляемому с помощью сумматора.

К этому же результату можно прийти иначе: сместим положение нуля на середину интервала 0 - 65535 и будем считать, что числа из первой половины 0-32767 положительные, а числа из второй половины 32769 - 65535 отрицательные. Тогда $100000000000011_2=32771_{10}$ -- код отрицательного числа, а $000000000000001_2=1_{10}$ -- код положительного числа. Это соответствует типу Integer на языке Pascal, при размещении чисел из интервала [-32768;32767] в 2 байтном машинном слове.

Пример. Рассмотрим операции 6+7=13, 14-8=6, 5*3=15, 12:4=3 в двоичных числах. Например, в десятичной системе: 5-3=2. Дополнительный код для 3 равен 7 (3+7=10). Так как 5+7=12, то отбрасывая старший разряд получаем 2. Тот же пример в двоичной системе: 0101-0011=0010; дополнительный код для 0011 равен 1101 (0011+1101=1 0000). Итак 0101+1101=10010. Старший разряд отбрасывается, получается $0010=2_{10}$.

1.6. Кодирование действительных чисел. Так как в ЭВМ для записи числа отводится конечное число разрядов, то количество возможных значений записываемых чисел конечно, например: 0.0000; 0.0001; 0.0002; ...; 0.3960; 0.3961; 0.3962; ... Действительные числа образуют континуум -- непрерывное множество. Машинные числа приближенно соответствуют отображаемым числам: числа 0.0000145 и 0.396131 будут восприниматься ЭВМ как 0.0000 и 0.3961, то есть приближенно. Это приводит к следующему:

1. Строгие соотношения между действительными числами $x_i$ оказываются нестрогими для их отображений $X_i$: если $x_1<x_2,$ то $X_1\le X_2$.

2. Так как отображения действительных чисел являются приближенными, то математическая обработка действительных чисел в ЭВМ ведется с погрешностью.

3. Математическое понятие нуля заменяется понятием "машинный нуль", как значения, которое меньше некоторой определенной величины.

Число называется нормализованным в системе счисления $p$, если оно представлено в виде $x=\pm M_p\cdot 10^{\pm k_p},$ где $M_p$ -- мантисса, лежащая в интервале $p^{-1}\le M_p<1,$ $k_p$ -- порядок числа.

Пример. Представление чисел в нормализованном виде: $2376,89_{10}=0,237689_{10}\cdot 10^{4_{10}}, -1011,01_2=-0,101101_2\cdot 2^{100_2};$ в форме чисел с фиксированной запятой: $+00721,35500; -10301,20260.$

Мантисса двоичного числа лежит в интервале $0,1_2=0,5_{10}\le M<1$, то есть содержит только цифры дробной части, которая всегда начинается на 1. Поэтому ноль в разряде целых, запятую, отделяющую дробную часть, и первую цифру дробной части мантиссы можно не сохранять, но восстанавливать при вычислениях. Пример размещения числа $-0,101110101\ldots 1110_2\cdot 2^{-1101011_2}$ в 32 разрядах:

Кодирование действительных чисел

Числа типа Real на языке Pascal размещаются 6 байтах, числа типа Extended занимают 10 байт.

1.7. Кодирование двоично-десятичных чисел. Для вывода чисел на экран используется двоично-десятичное представление чисел. В упакованном формате для каждой десятичной цифры отводится по 4 двоичных разряда (полбайта), при этом знак числа кодируется в крайнем правом полубайте числа (1100 -- знак $+$ и 1101 -- знак $-$).

При выполнении сложения и вычитания двоично-десятичных чисел используется упакованный формат: $ \vert$Цифра$ \vert$Цифра$ \vert$Цифра$\vert...\vert$ Цифра$ \vert$Знак$ \vert$. Упакованный формат используется обычно в ПК при выполнении операций сложения и вычитания двоично - десятичных чисел.

В распакованном формате для каждой десятичной цифры отводится по целому байту, при этом старшие полубайты (зона) каждого байта (кроме самого младшего) в ЭВМ заполняются кодом 0011, а в младших (левых) полубайтах обычным образом кодируются десятичные цифры. Старший полубайт (зона) самого младшего (правого) байта используется для кодирования знака числа.

Структура поля упакованного формата:

$ \vert$Зона$ \vert$Цифра$ \vert$Зона$\vert...\vert$Знак$ \vert$Цифра$\vert.$

Распакованный формат используется при вводе - выводе информации, а также при выполнении операций умножения и деления двоично-десятичных чисел.

Пример. Число $-193_{10}=-000110010011_{2-10}$ имеет следующий вид: а) в упакованном формате: $\vert001\vert 1001\vert011\vert 1101\vert$, б) в распакованном формате: $\vert011\vert001\vert011\vert 1001\vert 1101\vert011\vert$.

1.8. Кодирование команд. Машинная команда -- это элементарная инструкция, выполняемая ЭВМ автоматически без дополнительных указаний. Она состоит из двух частей: операционной и адресной.

В операционной части команды записан ее код, а в адресной -- один или несколько адресов ячеек памяти, в которых хранятся операнды (числа, участвующие в операции). Различают безадресные, одно-, двух-, трехадресные команды.

Команды могут кодироваться в двоичной, шестнадцатиричной и мнемонической (символической) формах. ЭВМ понимает только двоичную форму, при этом средняя по сложности программа состоит из тысяч битов. Для сокращения записи используют шестнадцатиричный код. Но это тоже не удобно: программист должен знать коды всех команд (около 100). Используется мнемонический (симоволический) код: каждая команда представлена совокупностью букв -- сокращений от английских названий команд. Симолическая программа транслируется ЭВМ в двоичный код и исполняется.

Структура трехадресной команды: $ \vert$КОП$\vert A1\vert A2\vert A3\vert,$ где КОП -- код операции, A1, A2 -- адреса ячеек, содержащих первый и второй операнды, A3 -- адрес ячейки, куда следует поместить результат выполнения операции.

Структура двух- и одноадресной команды: $ \vert$КОП$\vert A1\vert A2\vert,$ $ \vert$КОП$\vert A1\vert,$ где $A1, A2$ -- адреса ячеек ОЗУ, где хранятся операнды, и куда должен быть записан результат операции. Безадресная команда содержит только код операции, а информация для нее должна быть заранее помещена в определенные ячейки памяти.

Команда $ \vert$СЛ$\vert103\vert 5102\vert$ следует расшифровать так: "сложить число, записанное в ячейке 0103 памяти, с числом, записанным в ячейке 5102, а затем результат (то есть сумму) поместить в ячейку 0103." Команды $mov \, ax, bx$ и $add \, ax, bx$ помещают в регистр микропроцессорной памяти $ax$ содержимое ячейки $bx$, после чего складывают содержимое регистров $ax$ и $bx$ с последующей записью суммы в $ax.$

Все арифметические действия выполняются арифметико-логическим устройством. Сложение и вычитание чисел в двоично-десятичном представлении:

$ 123+345=468, \, \, 0001 0010 0011 + 0011 0100 0101 = 0100 0110 1000. $

1.9. Кодирование текстовой информации. Для представления текстовой информации используются 256 различных символов (строчные и прописные буквы русского и латинского алфавитов, знаки препинания, цифры и т.д.). Если считать, что использование каждого символа равновероятно, то его информационный вес: $ I=\log_2{256}= 8$ бит $= 1$ байт. Для двоичного кодирования 1 символа требуется 1 байт (8 битов). Тексты хранятся в памяти компьютера в двоичном коде и програмным способом преобразуются в изображение на экране. В текстовом режиме экран разбит на 25 строк по 80 символов в строке.

Информационный объем текстового сообщения в байтах численно равен количеству символов $N.$ В битах объем текстового файла равен: $V=8N.$


1.10. Кодирование графической информации. Форму представления на экране дисплея графического изображения, состоящего из отдельных точек (пикселей), называют растровой. Минимальным объектом в растровом графическом редакторе является точка (пиксель -- picture element). Разрешающая способность монитора (количество точек по горизонтали и вертикали), а также число возможных цветов каждой точки определяются типом монитора. Например: 640 $*$ 480= 307 200 точек, 800 $*$ 600= 480 000 точек. 1 пиксель черно-белого экрана кодируется 1 битом информации. Количество различных цветов $K$ и битовая глубина (число разрядов, используемых для кодировки цвета) $b$ связаны формулой: $K= 2^b.$

Зависимость цветовой палитры монитора от информационной емкости одного пикселя: 4 бита -- 16 цветов, 8 бит -- 256 цветов.

Объем памяти, необходимой для хранения графического изображения, занимающего весь экран, равен произведению количества пикселей (разрешающей способности) на число бит, кодирующих одну точку. Объем графического файла в битах определяется как произведение количества пикселей $N*M$ на разрядность цвета (битовую глубину) $C: V=N*M*C. $

Например, при разрешении $640*480$ и количестве цветов 16 (4 бита) объем памяти равен: $ 640*480*4=1228800$ (бит) или $1228800/8/1024=150$ Кбайт.

Объемы видеопамяти для мониторов с различными разрешающей способностью и цветовой палитрой [1] представлены ниже.


Бит/пиксель 4 бита 8 бит 16 бит 24 бита
Число цветов $2^4=16$ цв $2^8=256$ цв $2^{16}=65 536$ цв $2^{24}=16 777 216$ цв
640$*$480 150 Кбайт 300 Кбайт 600 Кбайт 900 Кбайт
800$*$600 234,4 Кбайт 468,8 Кбайт 937,6 Кбайт 1,4 Мбайт
1024$*$768 384 Кбайт 768 Кбайт 1,5 Мбайт 2,25 Мбайт
1280$*$1024 640 Кбайт 1,25 Мбайт 2,5 Мбайт 3,75 Мбайт

Ввод и хранение в ЭВМ технических чертежей, состоящих из отрезков, дуг, окружностей осуществляется в векторной форме. Минимальной единицей, обрабатываемой векторным графическим редактором, является объект (прямоугольник, круг, дуга). Для каждой линии указывается ее тип: тонкая, штрихпунктирная и т.д. Хранение информации в векторной форме на несколько порядков сокращает необходимый объем памяти по сравнению с растровой.

1.11. Цифровое кодирование аналогового сигнала. При оцифровке или дискретизации аналогового сигнала $X(t)$ происходит замена непрерывной функции $U=U(t)$ на интервале $[t_1, t_2]$ ломанной с большим количеством маленьких звеньев (ступенек). Это осуществляется путем развертки по времени OCи квантования по величине. Длительность ступенек равна шагу квантования по времени $\Delta t=1/f$, где $f$ -- частота отсчетов, а их величина кратна шагу квантования по величине $\Delta U.$ Величина каждой ступеньки представляется в двоичном коде, в результате чего получается массив $x={x_1, x_2, \ldots , x_n}$.

Теорема отсчетов В.А.Котельникова (1933 г.): Непрерывный сигнал может быть оцифрован и воссоздан без потери информации, если шаг развертки по времени не превышает половину периода максимальной гармоники сигнала: $ \Delta t\le 1/2f_{max}.$

Например, для оцифровки речевого сигнала с частотой до 5 кГц, частота отсчетов долна быть не менее 10 кГц.

Теорема квантования по величине: Для качественной оцифровки и воспроизведения непрерывного сигнала достаточно, чтобы шаг квантования по величине $\Delta U$ был меньше чувствительности приемного устройства $\delta U$.

Если глаз человека (приемник) различает 16 миллионов цветовых оттенков, то при квантовании цвета не имеет смысла делать больше градаций.

Преимущества цифрового представления сигнала: высокая помехоустойчивость, универсальность, простота и надежность устройств, обрабатывающих информацию.

1.12. Кодирование звуковой информации. Для записи и обработки аналогового сигнала с выхода микрофона осуществляется его оцифровка с помощью аналого-цифрового преобразователя. При этом они заменяются цифровыми значениями отдельных выборок, взятых через достаточно короткие промежутки времени $\Delta t.$ То есть непрерывный сигнал квантуется по величине и по времени, в результате чего получается поток логических 0 и 1, которые обрабатывает процессор. При 16-разрядном амплитудном кодировании непрерывный сигнал разбивается на $2^{16}=65 536$ ступеней квантования. В соответствии с теоремой отсчетов, частота квантования 44,1 кГц обеспечивает воспроизводимость всего звукового диапазона частот (до 20 кГц). При этом объем файла в битах равен $ V=f*r*t, $ где $f_{kvant}$ -- частота квантования, $r_{kvant}$ -- разрядность квантования по величине (число ступенек), $t$ -- время записи. Оцифрованный сигнал может быть преобразован в аналоговый с помощью цифроаналогового преобразователя.

1.13. Кодирование видеоинформации. Видеоинформация включает в себя последовательность кадров и звуковое сопровождение. Так как объемом звуковой составляющей видеоклипа можно пренебречь, то объем видеофайла примерно равен произведению количества информации в каждом кадре на число кадров. Число кадров вычисляется как произведение длительности видеоклипа $\Delta t$ на скорость кадров $v$, то есть их количество в 1 с: $ V=N*M*C*v*\Delta t. $ При разрешении 800*600 точек, разрядности цвета C=16, скорости кадров v=25 кадров/c, видеоклип длительностью 30 с будет иметь объем: $V=800*600*16*25*30=576*10^7 ($бит$)=72*10^7 ($байт$)=687 ($Мбайт$). $

1.14.  Аналоговое кодирование цифрового сигнала. Применяется при передаче данных по телефонным линиям связи и использует три способа модуляции:

1. Амплитудная модуляция: в соответствии с последовательностью передаваемых битов изменяется амплитуда синусоидальных колебаний, например, логической 1 соответствует большая амплитуда, а логическому 0 -- маленькая или отсутствие колебаний. OC

2. Частотная модуляция: в соответствии с передаваемыми битами изменяется частота колебаний: логическая 1 -- высокая частота, 0 -- низкая.

3. Фазовая модуляция: при переходе от логической 1 к логическому 0 и наоборот фаза колебаний изменяется на $180^0.$


1.15. Логические операции ЭВМ. Высказывание -- предложение, которое может быть истинным (логическая 1, true) или ложным (логический 0, false).


УМНОЖЕНИЕ СЛОЖЕНИЕ СЛОЖЕНИЕ ПО mod2 ИНВЕРСИЯ
A B A AND B A OR B A XOR B NOT A
0 0 0 0 0 1
0 1 0 1 1 1
1 0 0 1 1 0
1 1 1 1 0 0

Процессор ЭВМ состоит из логических элементов, выполняющих следующие операции: 1) логическое сложение ИЛИ (дезъюнкция "+", A OR B); 2) логическое умножение И (конъюнкция "*", A AND B); 3) логическое сложение по $mod\, 2$ (исключающее ИЛИ "$\otimes $", A XOR B); 4) логическое отрицание НЕ (инверсия, NOT A).

Перечисленные операции позволяют составить логические функции, которые в зависимости от значений аргументов A, B, C принимают два значения: истина (1) или ложь (0). Например: $f(A, B, C)=\bar A + B\otimes\bar{A}*C.$ Каждой логической функции соответствует цепь из логических элементов.

На основе логических элементов И, ИЛИ, НЕ построен процессор, осуществляющий математические и логические операции и управляющий работой ЭВМ, память ОЗУ, контроллеры и другие блоки ЭВМ.

1.16. Передача информации по сети. Информация, идущая от источника кодируется кодером и превращается преобразователем "коды-сигналы" в последовательность сигналов, поступающих в канал связи. Преобразователь "сигналы-коды" и декодер осуществляют обратное преобразование. На канал связи действуют шумы -- помехи, искажающие передаваемый сигнал, что компенсируется защитой от шумов.

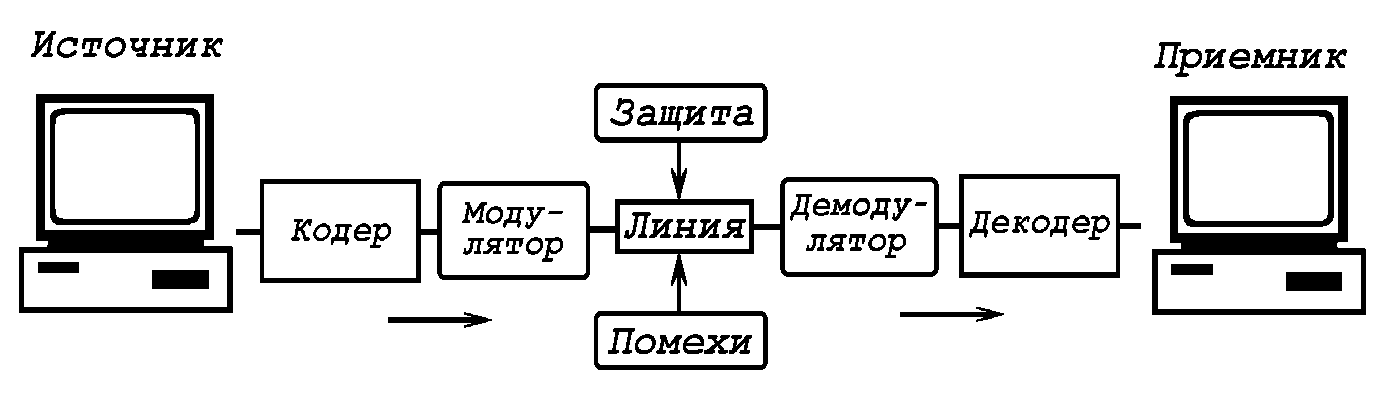
Передача информации по сети

Первичным называется алфавит, используемый в сообщении, которое выдает источник. Кодер преобразует сообщение, используя вторичный алфавит. Пусть первичный алфавит $A$ содержит $N$ знаков, а вторичный $B$ -- $M$ знаков. На каждый знак первичного и вторичного алфавита приходится средняя информация $I_A$ и $I_B$.

Передаваемое сообщение в первичном алфавите содержит $n$ знаков, а закодированное -- $m$ знаков, они несут количество информации $I(A)=nI_A$ и $I(B)=mI_B$. Кодирование будет обратимым, при условии неисчезновения информации, когда $I(A)\le I(B)$, то есть количество информации при обратимом кодировании не уменьшается. Тогда $I_A\le (m/n)I_B=K(A,B)I_B,$ где $K(A,B)=m/n$ -- длина кода, то есть среднее число знаков вторичного алфавита $B$, используемых для кодирования одного знака первичного алфавита $A.$ Итак, длина кода $K(A,B)\ge I_A/I_B$, а ее минимальное значение $K^{min}(A,B)=I_A/I_B.$ Если $I_A>I_B$, то $K(A,B)>1$, то есть одному знаку первичного алфавита соответствует несколько знаков вторичного. Относительная избыточность кода равна

\begin{displaymath}Q(A,B)=(K(A,B)-K^{min}(A,B))/K^{min}(A,B). \end{displaymath}

Проблема оптимизации кода состоит в нахождении метода кодирования, при котором средняя длина кода стремится к своему пределу: $K(A,B)\rightarrow K^{min}(A,B), Q\rightarrow 0,$ операция кодирования становится более эффективной. Ее решение позволит затратить на передачу сообщения меньше энергии и времени, а при его хранении использовать меньше поверхности носителя.

Первая теорема Шеннона (основная теорема о кодировании при отсутствии помех): При отсутствии помех возможно кодирование, при котором избыточность кода будет сколь угодно близка к нулю.

Если вторичный алфавит имеет 2 знака (двоичный код), то в случае оптимального кодирования средняя длина двоичного кода должна быть равна среднему информационному содержанию знака первичного алфавита.

На реальный канал связи действуют помехи, в результате чего возникают ошибки. Уровень достоверности передаваемого сообщения может быть определен как отношение числа ошибок к общему количеству знаков: $ D=n_{error}/n. $

Вторая теорема Шеннона: Если скорость передачи не превышает попускной способности канала связи с шумом, то всегда найдется способ кодирования, при котором сообщение будет передаваться с требуемой достоверностью.

Возможны два способа решения проблемы: 1) способ кодирования только устанавливает факт искажения собщения, что позволяет потребовать повторную передачу; 2) используемый код находит и автоматически исправляет ошибку передачи.